Piece Wise Functios to Determine Continuity

FINDING CONTINUITY OF PIECEWISE FUNCTIONS

About "Finding Continuity of Piecewise Functions"

Finding Continuity of Piecewise Functions :

Here we are going to how to find out the point of discontinuity for a piecewise function.

Finding Continuity of Piecewise Functions - Examples

Question 1 :

A function f is defined as follows :

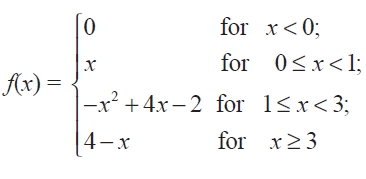
Is the function continuous?

Solution :

(i) First let us check whether the piece wise function is continuous at x = 0.

For the values of x lesser than 0, we have to select the function f(x)  =  0.

lim _x->0- f(x)  =lim_x->0- 0

  =  0 -------(1)

For the values of x greater than 0, we have to select the function f(x)  =  x.

lim_x->0+ f(x)  =  lim_x->0+ x

  =  0  -------(2)

lim _x->0 - f(x) = lim _x->0 + f(x)

Hence the function is continuous at x = 0.

(ii) Let us check whether the piece wise function is continuous at x = 1.

For the values of x lesser than 1, we have to select the function f(x)  =  x.

lim_x->1- f(x)  =  lim_x->1- 0

  =  1 -------(1)

For the values of x greater than 1, we have to select the function f(x)  =  -x² + 4x - 2.

lim_x->1+ f(x)  =  lim_x->1+ (-x² + 4x - 2)

  =  -1² + 4(1) - 2

=  -1 + 4 - 2

=  1  -------(2)

lim _x->1 - f(x) = lim _x->1 + f(x)

Hence the function is continuous at x = 1.

(iii) Let us check whether the piece wise function is continuous at x = 3.

For the values of x lesser than 3, we have to select the function f(x)  =  -x² + 4x - 2.

lim_x->3- f(x)  =  lim_x->3- -x² + 4x - 2

  =  -3² + 4(3) - 2

=  -9 + 12 - 2

=  -11 + 12

  =  1  -------(1)

For the values of x greater than 3, we have to select the function f(x)  =  4 - x

lim_x->3+ f(x)  =  lim_x->3+ 4 - x

=  4 - 3

=  1  -------(2)

lim _x->3 - f(x) = lim _x->3 + f(x)

Hence the function is continuous at x = 3.

Question 2 :

Find the points of discontinuity of the function f, where

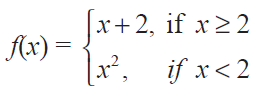
Solution :

For the values of x greater than 2, we have to select the function x + 2.

lim_x->2- f(x)  =  lim_x->2- x + 2

  =  2 + 2

       =  4  -------(1)

For the values of x lesser than 2, we have to select the function x².

lim_x->2+ f(x)  =  lim_x->2+ x²

  =  2²

       =  4-------(2)

lim _x->2 - f(x) = lim _x->2 + f(x)

The function is continuous at x = 2.

Hence the given piecewise function is continuous for all x ∈ R.

Question 3 :

Find the points of discontinuity of the function f, where

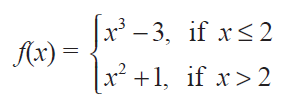
Solution :

For the values of x greater than 2, we have to select the function x² + 1

lim_x->2- f(x)  =  lim_x->2- x² + 1

  = 2 ²  + 1

       =  5  -------(1)

For the values of x lesser than 2, we have to select the function x³ - 3.

lim_x->2+ f(x)  =  lim_x->2+ x³- 3

  =  2³ - 3

=  8 - 3

       =  5-------(2)

lim _x->2 - f(x) = lim _x->2 + f(x)

The function is continuous at x = 2.

Hence the given piecewise function is continuous for allx ∈ R.

Question 4 :

Find the points of discontinuity of the function f, where

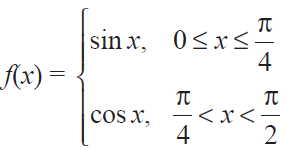
Solution :

Here we are going to check the continuity between 0 andπ/2.

For the values of x lesser than or equal toπ/4 , we have to choose the function sin x.

lim_{x-> π/4-} f(x)  =  lim_x-> π/4 ^- sin x

       =  sin (π/4)

=  1/ √2

For the values of x greater thanπ/4, we have to choose the function cos x .

lim_{x-> π/4+} f(x)  =  lim_x-> π/4 ⁺ cos x

       =  cos (π/4)

=  1/ √2

The function is continuous for all x ∈ [0, π/2).

After having gone through the stuff given above, we hope that the students would have understood, " Finding Continuity of Piecewise Functions"

Apart from the stuff given in " Finding Continuity of Piecewise Functions" , if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback tov4formath@gmail.com

We always appreciate your feedback.

© All rights reserved. onlinemath4all.com

toddpaidels.blogspot.com

Source: https://www.onlinemath4all.com/finding-continuity-of-piecewise-functions.html

Share this post